Sigarette a contatto

Il nostro viaggiatore claustrofobico della settimana scorsa farebbe bene a salire sull'ultimo vagone. A prima vista sembra che un'auto sia uguale all'altra; Ma poiché il tunnel si trova all'uscita della stazione, il treno continuerà ad accelerare quando vi entra, quindi l'ultimo vagone lo attraverserà più velocemente degli altri. Inoltre, come hanno sottolineato Salva Fuster e Francisco Montesinos, i passeggeri possono correre in avanti entrando nel tunnel, sommando così la loro velocità a quella del treno e ottenendo una velocità di attraversamento relativa più elevata.

Nel caso della bilancia a bracci disuguali, si tratta di una domanda trabocchetto (non dobbiamo dimenticare che si tratta di problemi posti da un bambino malizioso): la risposta è sì... purché si tratti della media geometrica e non della media aritmetica, come siamo soliti pensare quando diciamo semplicemente "la media".

Per quanto riguarda il problema delle piastrelle quadrate, sono stati sollevati numerosi commenti e diversi modi di affrontarlo. La più semplice, elegante e ingegnosa è quella proposta da Manuel Amorós. Chiamando a e b il numero di quadrati per lato di ogni quadrato e n il numero di pezzi, abbiamo:

n + 7 = a²

n – 10 = b²

con cui, sottraendo la seconda uguaglianza dalla prima:

(a + b)(a – b) = 17

da cui segue che a + b = 17, a – b = 1

quindi n = 74

Per coloro che trovano lo sviluppo troppo breve, ricordiamo che si tratta di “somma per differenza, differenza di quadrati”, e che 17, essendo primo, può essere scomposto solo in due fattori della forma 17 = 1 x 17.

E una soluzione altrettanto concisa ed elegante è quella offerta da María Luisa González alla variante con le tessere del domino:

Un quadrato con tessere del domino si forma con tessere X x 2X, quindi:

(X x 2X) – 1 = (X – 1)(2X – 2) + 13

La soluzione è che ho realizzato il primo quadrato con tessere 4x8 (e me ne mancava 1) e il secondo con 3x6 e me ne sono rimaste 13. Ho 31 tessere.

Enigmi cucinati

Nel gergo degli appassionati di enigmi logico-matematici, quando qualcuno scopre una soluzione migliore o diversa da quella "ufficiale", si dice che ha "cucinato" il problema. Ad esempio, Fuster e Montesinos hanno dato un'altra svolta al viaggiatore claustrofobico, sottolineando che, oltre a salire nell'ultimo vagone, possono anche correre in avanti per ridurre al minimo il tempo trascorso nel tunnel. E Luis Miguel Barros commenta che sua figlia quindicenne ha osservato che, poiché non è specificato nell'affermazione, la casella del domino non deve essere riempita: può essere una cornice di domino, il che porta a soluzioni nuove e interessanti. Ignacio Alonso sottolinea che i viaggiatori claustrofobici potrebbero preferire superare la spiacevole esperienza il più in fretta possibile, quindi opterebbero per la prima auto.

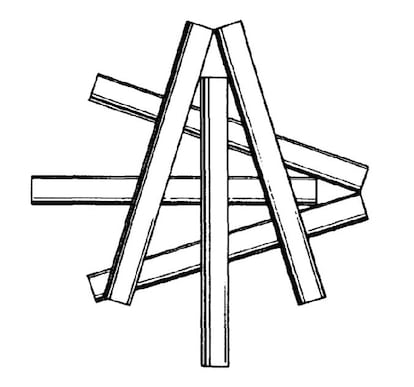
Uno dei problemi cotti più noti (di cui avevamo già parlato qualche anno fa) è quello delle sigarette a contatto. Per un certo periodo si pensò che 6 fosse il numero massimo di sigarette che si potevano disporre in modo che una toccasse tutte le altre, come mostrato nella figura; ma poi è apparsa una soluzione con 7 (riesci a trovarla?).

E dalla cucina semplice siamo passati all'alta cucina matematica, perché qualcuno ha chiesto quanti cilindri uguali si potrebbero mettere a contatto se non si potessero usare le estremità, cioè se fossero di lunghezza infinita (secondo voi quanti ce ne sono?).

E ancora una volta, quello che sembrava un semplice divertimento matematico si è rivelato essere correlato ai materiali auxetici, ovvero quelli con un coefficiente di Poisson negativo, il che significa che, a differenza di un elastico o di una gomma da masticare, si espandono quando vengono allungati anziché restringersi. Ma questo è un altro articolo...