Wilde Tauben

Letzte Woche haben wir uns gefragt, wie viele kleinere gleichseitige Dreiecke mindestens benötigt werden, um ein gleichseitiges Dreieck zu überdecken. Diese kleineren Dreiecke müssen nicht gleich groß sein und können sich überlappen. Die Antwort lautet 3, und wir gelangen zu dieser Antwort, indem wir die kleinste Möglichkeit ausschließen: Bei 3 ist es offensichtlich möglich, und es ist nicht schwer zu zeigen (wie?), dass es bei 2 nicht möglich ist.

Zum Problem der 5 Punkte eines gleichseitigen Dreiecks wurden verschiedene Ansätze vorgeschlagen; der eingängigste ist der von Francisco Montesinos:

„Indem wir die Mittelpunkte der Seiten des ursprünglichen gleichseitigen Dreiecks verbinden, erhalten wir vier gleichseitige Dreiecke mit einer Seitenlänge von 1/2 m. Zwei der fünf gegebenen Punkte liegen zwangsläufig innerhalb desselben Dreiecks wie die reduzierten Punkte, sodass ihr Abstand d nicht d>1/2 sein kann.“

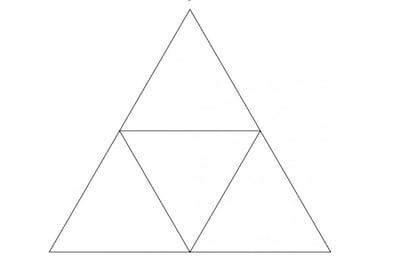
Durch die Aufteilung des ursprünglichen Dreiecks in vier gleich große Dreiecke entsteht ein Taubenschlag mit vier Abteilen, von denen jedes fünf Tauben bzw. Punkte aufnehmen muss. Und der größte Abstand, der in einem gleichseitigen Dreieck mit einer Seitenlänge von ½ m bestehen kann, entspricht genau der Länge der Seite, sodass zwei Punkte innerhalb des Dreiecks höchstens ½ m voneinander entfernt sein können (und offensichtlich die Eckpunkte des Dreiecks sind).

Die von Rafael Granero bereitgestellte Lösung ist etwas komplizierter , aber nicht weniger interessant:

„Sicherlich gibt es vier Punkte, die am weitesten entfernt sein müssen, und man könnte sogar sagen, dass diese vier Punkte so weit voneinander entfernt sind, wie es nur sein kann: die drei Scheitelpunkte und der Mittelpunkt. Der Mittelpunkt ist 57,7 cm von jedem der drei Scheitelpunkte entfernt. Jede noch so kleine Bewegung des Mittelpunkts verringert unvermeidlich den Abstand zu einem oder zwei Scheitelpunkten. Und das Gleiche gilt für jeden der Punkte an den Scheitelpunkten in Bezug auf die anderen drei Punkte. Die einzigen Punkte, die weiter als 50 cm vom Mittelpunkt entfernt sind, befinden sich außerhalb eines Kreises mit Radius 50, dessen Mittelpunkt der Mittelpunkt des gleichseitigen Dreiecks ist. Aber in jeder der drei Zonen sind alle Punkte weniger als 8 cm vom am weitesten entfernten Punkt, dem Scheitelpunkt, entfernt. Es gibt also keine Möglichkeit, einen fünften Punkt zu finden, der weiter als 50 cm von den anderen vier entfernt ist.“

Ganz nebenbei wurde noch die Frage gestellt, wie unwahrscheinlich es ist, 13 Mal würfeln zu müssen, um 3 gleiche Zahlen zu erhalten und hier die Antwort von Juan Zubieta:

Die Wahrscheinlichkeit, die 13 zu würfeln, ist der Quotient der möglichen Permutationen mit sechs Zahlenpaaren (12!/2^6) und allen möglichen Würfelfolgen (6^12). Das Ergebnis lautet: 1925/559872 (ungefähr eine Chance von 1 zu 291). (Zur Erinnerung: Es geht nicht darum, eine bestimmte Zahl wie die 6 dreimal zu würfeln, sondern darum, dass eine Zahl mindestens dreimal vorkommt.)

Taubenschlag mit hohem Risiko

Nach der Schulung der letzten Wochen und insbesondere für diejenigen, die glauben, dass das Schubladenprinzip eine Binsenweisheit ist, die nur auf die einfachsten Probleme anwendbar ist, hier ein Klassiker, der die Aufmerksamkeit von Paul Erdös selbst verdient hat:

Zeigen Sie anhand der Menge {1, 2, …, 2n}, dass es in jeder Teilmenge von n+1 Zahlen mindestens zwei Zahlen gibt, von denen eine ein Vielfaches der anderen ist.

Versuchen Sie nicht, das Problem während der heißesten Stunden zu lösen: Die Tauben in diesem Hochrisikoschlag könnten Ihre Gehirnzellen braten.