Sigara teması

Geçtiğimiz haftaki klostrofobik yolcumuzun son vagona binmesi akıllıca olacaktır. İlk bakışta bir arabanın diğerine benzediği düşünülebilir; Ancak tünel istasyonun çıkışında olduğundan, tren tünele girerken hala hızlanıyor olacağından, son vagon diğerlerinden daha hızlı geçecektir. Ayrıca Salva Fuster ve Francisco Montesinos'un da belirttiği gibi, yolcular tünele girerken öne doğru koşabilecekleri için, kendi hızları trenin hızına eklenecek ve bu da daha yüksek bir geçiş hızı sağlayacaktır.

Eşit olmayan kol terazisi durumunda, bu bir tuzak sorudur (bunların kötü niyetli bir çocuğun sorduğu problemler olduğunu unutmamalıyız): cevap evet... geometrik ortalama olduğu sürece, aritmetik ortalama değil, çünkü biz basitçe "ortalama" dediğimizde bunu düşünürüz.

Kare fayans sorunu ile ilgili olarak çok sayıda yorum yapılmış ve farklı çözüm yolları ortaya çıkmıştır. En sade, en zarif ve en yaratıcı olanı Manuel Amorós'un önerisidir. Her bir karenin bir kenarındaki kare sayısına a ve b , parça sayısına n dersek, şunu elde ederiz:

n + 7 = a²

n – 10 = b²

bununla birlikte, ikinci eşitliği birinciden çıkararak:

(a + b)(a – b) = 17

bundan a + b = 17, a – b = 1 olduğu sonucu çıkar

yani n = 74

Açıklamayı çok kısa bulanlar için, “farklara göre toplama, kareler farkı” kavramını ve 17’nin asal sayı olması nedeniyle yalnızca 17 = 1 x 17 biçimindeki iki çarpanına ayrılabileceğini hatırlayalım.

Ve aynı derecede öz ve zarif bir çözüm de María Luisa González'in dominolu versiyona sunduğu çözümdür:

Domino taşlarından oluşan bir kare, X x 2X domino taşıyla oluşturuluyorsa:

(X x 2X) – 1 = (X – 1)(2X – 2) + 13

Çözüm şu: İlk kareyi 4x8'lik parçalarla yaptım (ve 1 tanesi eksikti) ve ikinciyi 3x6'lık parçalarla yaptım ve 13 tane kaldı. 31 tane taşım var.

Pişmiş bilmeceler

Mantık-matematik bulmaca meraklılarının jargonunda, birisi "resmi" çözümden daha iyi veya farklı bir çözüm bulduğunda, problemi "pişirdiği" söylenir. Örneğin Fuster ve Montesinos, klostrofobik yolculara, son vagona binmenin yanı sıra tünelde geçirilen süreyi en aza indirmek için ileri doğru koşabileceklerini belirterek başka bir bakış açısı getirmişlerdir. Luis Miguel Barros ise, on beş yaşındaki kızının, açıklamada belirtilmediği için domino karesinin dolu olması gerekmediğini, bunun bir domino çerçevesi olabileceğini, bunun da yeni ve ilginç çözümlere yol açtığını gözlemlediğini belirtiyor. Ignacio Alonso ise klostrofobik gezginlerin, yaşadıkları tatsız deneyimden olabildiğince çabuk kurtulmak isteyebileceklerini, bu nedenle de ilk arabayı tercih edeceklerini belirtiyor.

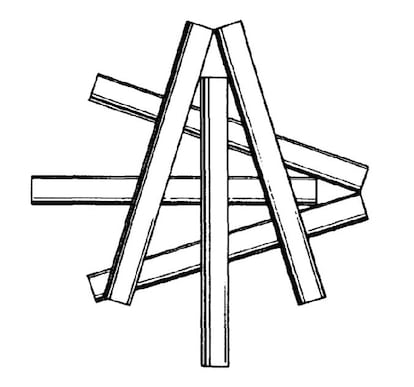
En meşhur pişmiş sorunlardan biri (birkaç yıl önce bahsetmiştik) sigarayla temas sorunudur. Bir zamanlar, şekilde gösterildiği gibi, her sigaranın diğerlerine değecek şekilde düzenlenebileceği en fazla sigara sayısının 6 olduğu düşünülüyordu; ama sonra 7'li bir çözüm çıktı (bulabilir misin?).

Ve basit yemek pişirmeden yüksek matematiksel mutfağa geçtik, çünkü biri uçları kullanılamayacaksa, yani sonsuz uzunluktaysa (sizce kaç tane olduğunu düşünüyorsunuz?) kaç tane eşit silindirin birbirine temas ettirilebileceğini sormuştu.

Ve bir kez daha, basit matematiksel eğlence gibi görünen şeyin, negatif Poisson oranına sahip olan, yani lastik bant veya sakızdan farklı olarak, gerildiklerinde daralmak yerine genişleyen auxetik malzemelerle ilgili olduğu ortaya çıktı. Ama bu başka bir yazının konusu...