Свирепые голуби

На прошлой неделе мы спрашивали себя, сколько меньших равносторонних треугольников нужно, как минимум, чтобы покрыть равносторонний треугольник. Эти меньшие треугольники не обязательно должны быть равными и могут перекрываться. Ответ — 3, и мы приходим к нему, исключая наименьшую возможность: это, очевидно, возможно с 3, и несложно показать (как?), что это невозможно с 2.

Относительно задачи о пяти вершинах равностороннего треугольника были предложены различные подходы; наиболее «узким» является подход Франсиско Монтесиноса:

«Соединив середины сторон исходного равностороннего треугольника, мы получим 4 равносторонних треугольника со сторонами 1/2 м. Две из 5 заданных точек обязательно будут находиться внутри того же треугольника уменьшенных, поэтому их расстояние d не может быть d>1/2».

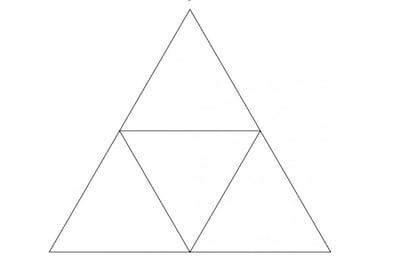
Действительно, разделив исходный треугольник на 4 равных треугольника, мы создаем голубятню с 4 ячейками, каждая из которых должна вмещать 5 голубей, или точек. И наибольшее расстояние, которое может существовать в равностороннем треугольнике со стороной 1/2 м, как раз равно длине стороны, поэтому любые две точки, расположенные внутри него, могут находиться на расстоянии не более 1/2 м друг от друга (и, очевидно, являются вершинами треугольника).

Решение, предложенное Рафаэлем Гранеро, несколько сложнее , но не менее интересно:

«Конечно, есть четыре точки, которые должны быть дальше всего, и можно даже сказать, что, если взять четыре точки, они находятся дальше всего друг от друга: три вершины и центр. Центр находится на расстоянии 57,7 см от любой из трех вершин. Любое перемещение, каким бы малым оно ни было, точки, расположенной в центре, неизбежно уменьшит расстояние до одной или двух вершин. И то же самое справедливо для каждой из точек, расположенных в вершинах, по отношению к остальным трем точкам. Единственные точки, которые находятся дальше, чем в 50 см от центральной точки, — это те, которые находятся за пределами круга радиусом 50 с центром в центре равностороннего треугольника. Но в каждой из трех зон все точки находятся менее чем в 8 см от самой дальней точки, которая является вершиной, поэтому нет способа найти пятую точку, которая находится дальше, чем в 50 см от остальных четырех».

Как бы между прочим, был задан вопрос о том, насколько маловероятно, что придется бросать кубик 13 раз, чтобы получить 3 одинаковых числа, и вот ответ Хуана Зубиеты:

«Вероятность выпадения броска 13 равна частному возможных перестановок с 6 парами чисел (12!/2^6) и всеми возможными последовательностями бросков (6^12). Результат: 1925/559872 (приблизительно один шанс из 291)». (Помните, речь идет не о получении определенного числа, например 6, 3 раза, а скорее о том, чтобы некоторое число выпало по крайней мере 3 раза.)

Голубятня с высоким риском

После обучения последних нескольких недель, и особенно для тех, кто считает, что принцип ящика — это трюизм, применимый только к самым простым проблемам , вот классика, которая заслужила внимание самого Пауля Эрдёша:

Для заданного набора {1, 2, …, 2n} покажите, что в любом подмножестве из n+1 чисел найдутся по крайней мере два таких, что одно из них кратно другому.

Не пытайтесь решить эту задачу в самые жаркие часы: голуби в этом опасном голубятне могут поджарить ваши мозговые клетки.