Cigarettes en contact

Notre voyageur claustrophobe de la semaine dernière serait bien avisé de monter dans le dernier wagon. À première vue, il semble qu’une voiture soit identique à une autre ; Mais comme le tunnel se trouve à la sortie de la gare, le train accélérera encore en y entrant, donc le dernier wagon le traversera plus vite que les autres. De plus, comme l'ont souligné Salva Fuster et Francisco Montesinos, les passagers peuvent courir vers l'avant en entrant dans le tunnel, leur propre vitesse s'ajoutera donc à celle du train, ce qui donnera une vitesse de traversée relative plus élevée.

Dans le cas de la balance à bras inégaux, c’est une question piège (il ne faut pas oublier qu’il s’agit de problèmes posés par un enfant malicieux) : la réponse est oui… à condition qu’il s’agisse de la moyenne géométrique et non de la moyenne arithmétique, comme on a tendance à le penser quand on dit simplement « la moyenne ».

Concernant le problème des tuiles carrées, il a donné lieu à de nombreux commentaires et à différentes manières de l'aborder. Le plus simple, le plus élégant et le plus ingénieux est celui proposé par Manuel Amorós. En appelant a et b le nombre de carrés par côté de chaque carré, et n le nombre de pièces, nous avons :

n + 7 = a²

n – 10 = b²

avec laquelle, en soustrayant la deuxième égalité de la première :

(a + b)(a – b) = 17

d'où il résulte que a + b = 17, a – b = 1

donc n = 74

Pour ceux qui trouveraient le développement trop bref, rappelons celui de « somme par différence, différence de carrés », et que 17, étant premier, ne peut être décomposé qu'en deux facteurs de la forme 17 = 1 x 17.

Et une solution tout aussi concise et élégante est celle proposée par María Luisa González à la variante avec des dominos :

Un carré avec des dominos est formé avec X x 2X dominos, donc :

(X x 2X) – 1 = (X – 1)(2X – 2) + 13

La solution est que j'ai fait le premier carré avec des tuiles 4x8 (et il m'en manquait 1) et le deuxième avec 3x6 et il m'en restait 13. J'ai 31 tuiles.

Devinettes cuisinées

Dans le jargon des passionnés de casse-têtes logico-mathématiques, lorsque quelqu'un découvre une solution meilleure ou différente de la solution « officielle », on dit qu'il a « cuit » le problème. Par exemple, Fuster et Montesinos ont donné une autre tournure au voyageur claustrophobe en soulignant qu'en plus de monter dans le dernier wagon, ils peuvent courir vers l'avant pour minimiser le temps passé dans le tunnel. Et Luis Miguel Barros commente que sa fille de quinze ans a observé que, comme cela n'est pas spécifié dans la déclaration, le carré de dominos n'a pas besoin d'être rempli : il peut s'agir d'un cadre de dominos, ce qui conduit à des solutions nouvelles et intéressantes. Et Ignacio Alonso souligne que les voyageurs claustrophobes pourraient préférer surmonter cette expérience désagréable le plus rapidement possible, ils opteraient donc pour la première voiture.

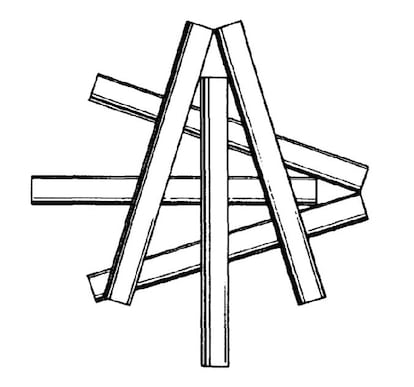
L’un des problèmes cuits les plus connus (dont nous avons déjà parlé il y a quelques années) est celui des cigarettes en contact. Pendant un temps, on pensait que 6 était le nombre maximum de cigarettes qui pouvaient être disposées de manière à ce que chacune touche toutes les autres, comme le montre la figure ; mais ensuite une solution avec 7 est apparue (pouvez-vous la trouver ?).

Et de la cuisine simple, nous sommes passés à la haute cuisine mathématique, car quelqu'un a demandé combien de cylindres égaux pourraient être mis en contact si leurs extrémités ne pouvaient pas être utilisées, c'est-à-dire s'ils étaient de longueur infinie (combien pensez-vous qu'il y en ait ?).

Et une fois de plus, ce qui semblait être un simple divertissement mathématique s'est avéré être lié aux matériaux auxétiques, qui sont ceux avec un coefficient de Poisson négatif, ce qui signifie que, contrairement à un élastique ou à un chewing-gum, ils se dilatent lorsqu'ils sont étirés plutôt que de se rétrécir. Mais c'est un autre article...