Zigaretten im Kontakt

Unser klaustrophobischer Reisender von letzter Woche wäre gut beraten, in den letzten Wagen einzusteigen. Auf den ersten Blick scheint ein Auto dem anderen zu gleichen; Da sich der Tunnel jedoch am Ausgang des Bahnhofs befindet, beschleunigt der Zug bei der Einfahrt noch immer, sodass der letzte Wagen ihn schneller durchquert als die anderen. Darüber hinaus können die Passagiere, wie Salva Fuster und Francisco Montesinos hervorgehoben haben, beim Einfahren in den Tunnel vorwärts rennen, so dass sich ihre eigene Geschwindigkeit zu der des Zuges addiert, was zu einer höheren relativen Durchfahrtsgeschwindigkeit führt.

Im Fall der ungleicharmigen Waage handelt es sich um eine Fangfrage (wir dürfen nicht vergessen, dass es sich hierbei um Aufgaben eines böswilligen Kindes handelt): Die Antwort lautet ja … solange es sich um den geometrischen Mittelwert handelt und nicht um den arithmetischen Mittelwert, wie wir gerne denken, wenn wir einfach „der Mittelwert“ sagen.

Zum Problem der quadratischen Kacheln gab es zahlreiche Kommentare und unterschiedliche Lösungsansätze. Der einfachste, eleganteste und genialste Vorschlag ist der von Manuel Amorós. Wenn wir a und b als die Anzahl der Quadrate pro Seite jedes Quadrats und n als die Anzahl der Teile bezeichnen, erhalten wir:

n + 7 = a²

n – 10 = b²

wobei die zweite Gleichheit von der ersten subtrahiert wird:

(a + b)(a – b) = 17

woraus folgt, dass a + b = 17, a – b = 1

also n = 74

Für diejenigen, denen die Entwicklung zu kurz erscheint, sei an die „Summe durch Differenz, Differenz der Quadrate“ erinnert, und daran, dass 17 als Primzahl nur in zwei Faktoren der Form 17 = 1 x 17 zerlegt werden kann.

Und eine ebenso prägnante wie elegante Lösung bietet María Luisa González für die Variante mit Dominosteinen:

Ein Quadrat mit Dominosteinen wird mit X x 2X Dominosteinen gebildet, daher:

(X x 2X) – 1 = (X – 1)(2X – 2) + 13

Die Lösung besteht darin, dass ich das erste Quadrat mit 4x8-Kacheln gemacht habe (und mir fehlte 1) und das zweite mit 3x6 und mir blieben 13 übrig. Ich habe 31 Kacheln.

Gekochte Rätsel

Im Jargon der logisch-mathematischen Rätsel-Enthusiasten heißt es: Wenn jemand eine bessere oder andere Lösung als die „offizielle“ findet, sagt man, er habe das Problem „gekocht“. Fuster und Montesinos haben dem klaustrophobischen Reisenden beispielsweise eine weitere Wendung gegeben, indem sie darauf hinwiesen, dass Reisende nicht nur in den letzten Wagen einsteigen, sondern auch nach vorne rennen können, um die Zeit im Tunnel zu minimieren. Und Luis Miguel Barros bemerkt, dass seine fünfzehnjährige Tochter bemerkt habe, dass das Dominoquadrat nicht ausgefüllt werden müsse, da es in der Aussage nicht spezifiziert sei: Es könne ein Rahmen aus Dominosteinen sein, der zu neuen und interessanten Lösungen führe. Und Ignacio Alonso weist darauf hin, dass Reisende mit Klaustrophobie die unangenehme Erfahrung vielleicht so schnell wie möglich hinter sich bringen möchten und sich deshalb für das erste Auto entscheiden würden.

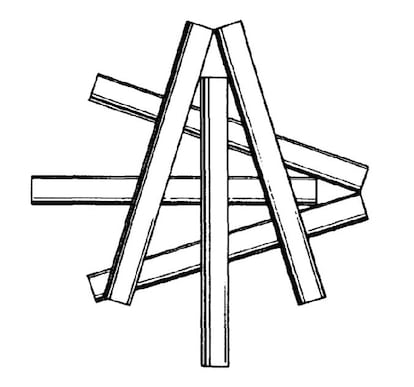
Eines der bekanntesten Kochprobleme (über das wir bereits vor einigen Jahren gesprochen haben) ist der Kontakt mit Zigaretten. Eine Zeit lang dachte man, dass 6 die maximale Anzahl an Zigaretten sei, die man so anordnen könne, dass jede Zigaretten alle anderen berührt, wie in der Abbildung gezeigt. aber dann erschien eine Lösung mit 7 (können Sie sie finden?).

Und vom einfachen Kochen sind wir zur gehobenen mathematischen Küche übergegangen, weil jemand gefragt hat, wie viele gleiche Zylinder in Kontakt gebracht werden könnten, wenn ihre Enden nicht verwendet werden könnten, das heißt, wenn sie unendlich lang wären (was glauben Sie, wie viele es sind?).

Und wieder einmal stellte sich heraus, dass das, was wie ein einfacher mathematischer Spaß aussah, mit auxetischen Materialien zusammenhängt. Das sind Materialien mit einer negativen Poissonzahl , was bedeutet, dass sie sich im Gegensatz zu einem Gummiband oder Kaugummi beim Dehnen ausdehnen, anstatt sich zusammenzuziehen. Aber das ist ein anderer Artikel …